El inLab FIB está colaborando actualmente en un proyecto llamado Intelibus, conjuntamente con la empresa de movilidad Autocorb y la compañía TIC de desarrollo software Geoactio, para desarrollar un sistema de predicción de la ocupación de pasajeros en los buses.
El inLab FIB está colaborando actualmente en un proyecto llamado Intelibus, conjuntamente con la empresa de movilidad Autocorb y la compañía TIC de desarrollo software Geoactio, para desarrollar un sistema de predicción de la ocupación de pasajeros en los buses. Debido a la pandemia de la Covid-19, se ha acelerado la implementación de esta funcionalidad, ya que puede ayudar a frenar los contagios y evitar aglomeraciones: si se informa a la gente de cómo irán de llenos los buses con antelación, los usuarios podrán optar por viajar en autobuses que vayan más vacíos. En este artículo del blog explicamos qué métodos y algoritmos de predicción utilizamos y, aprovecharemos para entrar un poco en detalle en modelos de machine learning como las redes neuronales.
En el campo de la inteligencia artificial hay muchas maneras de abordar un problema de predicción como este: mediante simulación, estimando la demanda, implementando heurísticas, utilizando machine learning/deep learning, etc. Dado que las empresas de autobuses suelen guardar datos e históricos de los viajes de cada autobus, se abre la posibilidad de abordar el problema con aprendizaje supervisado (supervised learning), es decir, entrenar modelos con datos etiquetadas con el que queremos predecir . En el proyecto de Intelibus disponemos de datos provenientes de cámaras 3D del interior de los autobuses que cuentan las personas que suben y bajan en cada parada. Si juntamos estos datos con información de las diferentes líneas de autobuses, información de calendario e históricos de validaciones de los pasajeros, ya tendríamos los datos necesarios para ser capaces de entrenar redes neuronales que predigan de empleo en cada parada.
¿Qué es entrenar un modelo?
Cuando hablamos de entrenar una red neuronal, lo que queremos en realidad es ajustar los parámetros de una función (red neuronal) para que aprenda una tarea concreta, es decir, que aprenda a mapear unos inputs a outputs. Esto se consigue utilizando grandes cantidades de datos para ir minimizando el error de predicción del modelo respecto a éstas. ¿Os suena la «regla de la cadena» que os enseñaron para derivar y pensabais que nunca más oiríais hablar de ella?, pues bien, el proceso de entrenamiento de una red neuronal se basa principalmente en la ingeniosa aplicación de esta regla, la que nos permite calcular cómo se deben ir modificando los parámetros de la red para minimizar el error de predicción iterativamente.

En nuestro caso, queremos que el modelo aprenda a calcular la ocupación de los buses en cada una de las paradas por donde pasan. De modo que al modelo le debemos dar como input una representación numérica (vectores) de la información del bus, la parada, el calendario, etc. y queremos que nos devuelva el número de pasajeros que habrá, tal como se muestra en la siguiente imagen. Con históricos de unos meses anteriores ya podemos llegar a obtener una precisión de predicción bastante buena.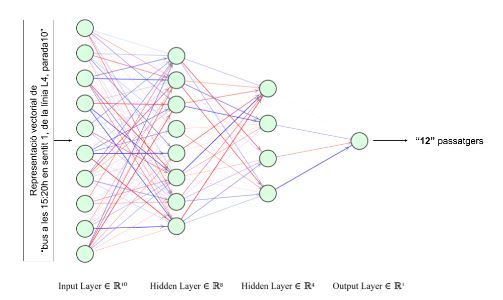
La gracia de utilizar redes neuronales es que nos permiten, con un único modelo, poder predecir sobre cualquiera de las líneas de bus en cada una de las paradas, sin tener que hacer un modelo o algoritmo especializado para cada una de las líneas. Esto simplifica la complejidad de implementación a la hora de llevarlo a producción y permite también aplicarlo en otras ciudades fácilmente, donde las líneas y las paradas serán completamente diferentes.
Series temporales: Redes neuronales recurrentes
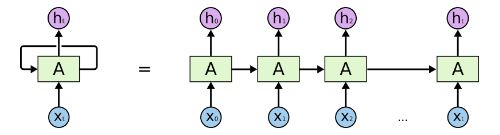
Sin embargo, podemos llegar a hacerlo mejor. El modelo que acabamos de presentar no tiene en cuenta la ocupación previa de las paradas anteriores, la cual es una información muy relevante y, saberla puede condicionar mucho la ocupación de la próxima parada. Para estos tipos de problemas que se tratan secuencias hay un tipo de redes neuronales llamadas redes recurrentes (Recurrente Neural Networks), que nos permiten trabajar con series temporales teniendo en cuenta los valores anteriores de empleo para predecir la de la siguiente parada. Para hacerse una idea de cómo son, la siguiente imagen muestra un esquema simplificado de cómo es el flujo de información de los inputs hasta los outputs. Lo que hacen, en resumen, es ir codificando la información de las paradas previas de forma compacta para, finalmente, obtener un vector (ht) que contiene toda la información comprimida de la secuencia a partir del cual podemos predecir el valor de empleo siguiente. Así pues, con esta arquitectura de red neuronal obtenemos mejores resultados, ya que el modelo puede llegar a captar los cambios y patrones en el empleo de pasajeros a lo largo del tiempo.
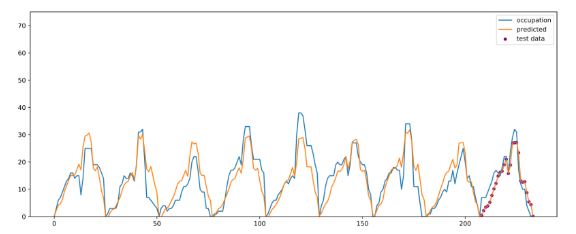
En conclusión, vemos que estos modelos basados en redes neuronales son muy versátiles, y permiten resolver una gran diversidad de problemas de manera muy eficaz y precisa si disponemos de los datos necesarios.
Referencias
Predicció d’ocupacions a l’autobús (https://www.autocorb.com/prediccio-ocupacions-bus/)
Neural Networks and Deep Learning (http://neuralnetworksanddeeplearning.com/)
Understanding Neural Networks (https://towardsdatascience.com/understanding-neural-networks-19020b758230)
Hochreiter, Sepp & Schmidhuber, Jürgen. (1997). Long Short-term Memory. Neural computation. 9. 1735-80. 10.1162/neco.1997.9.8.1735.